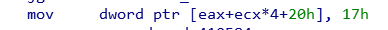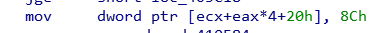软件常用加密算法并简单逆向识别知识
前言
想作为分析勒索病毒前的密码学接触.有些太难的算法,弟弟属实吃力,就不献丑了.可能也存在未察觉的错误,希望各位帮忙提出来,避免误导他人.谢谢师傅们.
常用加解密算法的逆向分析中的识别,不做过多算法原理上的叙述,别人讲的好多了.站在巨人的肩膀上.
这篇文章只作为特征查找用来辅助平时分析用.
两种工具ida插件FindCrypt2和peid的KANA进行算法识别是很好用的.
Base64
历史发展
base64最早就是用来邮件传输协议中的,原因是邮件传输协议只支持 ascii 字符传递,因此如果要传输二进制文件,如:图片、视频是无法实现的。因此 base64就可以用来将二进制文件内容编码为只包含 ascii 字符的内容,这样就可以传输了.
简单来说为了兼容各种数据格式.
基本原理
采用每三字节置换为四字节的方式,3x824位二进制转换为4x6的方式,前两位用0填充.字符不够转换的话,空字符=填充.(1字节或二字节输入,那么只能使用输出的2个或3个字符)
使用字符表"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"置换
Base24:"BCDFGHJKMPQmogRTVWXY2346789"
Base32:"ABCDEFGHJKLMNOPQRSTUVWXYZ234567"
Base60:"0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwx"
逆向初探
Findcrypt2和KANAL都能是识别出置换表.
所以先关注置换表,然后关注下相关的位运算操作,可能就是base相关算法.
编码伪代码部分:
魔改Base64
- 置换表里的字符顺序变化或者修改置换表
- 将置换表分成几个不连续的部分,根据偏移进行对应的索取,或者进行加密.
嘛 具体问题具体分析
单向散列
用的比较多的就是MD5和SHA-1等算法
MD5
特征
这里和加密与解密上都讲的挺好的,我做些我需要的东西的提炼
填充消息使其长度与
448 mod 512同余,是为了后面填充64位的长度.填充方法:附一个
1在消息后面,然后用0填充,填充长度0<x<=512初始化最开始需要使用
0x67452301,0xefcdab89,0x98badcfe,0x10325476进行初始化然后进行数据处理,相关细节看书和源码就好.需要使用左移数组
{ 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7,12, 17, 22, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20,4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 6, 10,15, 21, 6, 10, 15, 21, 6, 10, 15, 21,, 6, 10, 15, 21 }和64个存放32位字节的加法常数数组,由
2^32 * (abs(sin(i)))得出,i的范围1到64.{ 0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501, 0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821, 0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8, 0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a, 0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70, 0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665, 0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1, 0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391 };512位消息分组为
16组 x 32位,进行4*16次运算128位散列值。
逆向识别
FindCrypt2和peid的KANA都是识别加法常数
采用加密与解密中的MD5KeyGen.exe进行分析学习
寄存器初始化
MD5计算部分伪代码每使用16个硬编码常量,都会发现算法的改变.详细算法看上面第四点
这样简单的确定了是
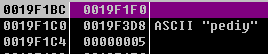
MD5算法,然后可以从进行回溯,ida识别有点问题,汇编看了下二者相等.v11是置换表说明v4可能就是计算后的值,再动态调试可知,过滤掉前面的判断进行MD5计算的值为说明在中途加了
www.pediy.com字符串,sub_4012E0集成了字符串添加和拷贝的字符大小刚好等于原字符串差64位的大小时,拷贝并直接计算MD5的功能.大概的流程差不多分析出来了,基本上修改下原版
MD5的算法就能写出注册机了
魔改
- 可能会改变四个常数
- 改变输入后的字符,添加或者做某些运算等等
- hash处理过程可能改变
SHA算法
散列值长度:SHA-1 160位 SHA-256256位 SHA-384 384位 SHA-512512位
SHA-2包括SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256
SHA-1
原理参考:https://www.wosign.com/News/news_2018121101.htm 讲的很详细
特征
消息填充和
MD5一样,512位为一组,然后16组x32位,然后扩充位80组x32位,进行4*20次运算使用该函数进行计算
A,B,C,D,E←[(A<<5)+ ft(B,C,D)+E+Wt+Kt],A,(B<<30),C,D,f函数伪代码在下方使用常数
初始化寄存器的
hash值
逆向初探SHA-1加密
使用加密与解密的6.1.2示例程序
FindCrypt插件识别出SHA-1常量对输入进行判断,
Name不为空,Serial为20位基本流程
注册机
成功
计算函数的部分伪代码参考
总结
要注意字节与位转换函数,不太熟悉容易迷惑
对称加密
RC4
RC4生成一种被称为密钥流的伪随机流.它与加密的数据长度相等.密钥流与数据同位异或进行加解密.密钥流生成分为两个部分KSA与PRGA.
the key-scheduling Algorithm (KSA) 密钥调度算法
按照升序
0,1,2,3,4.....,254,255初始化一个256字节数组S.使用密钥填充一个256字节数组
T,长度不够的话,轮转填入,直到填满.对数组
S进行打乱.int j = 0; for (i = 0;i<256;i++){ j =(j+S[i]+T[i])%256; swap(S[i],S[j]); }the Pseudo-Random Generation Algorithm (PRGA) 伪随机生成算法
int i, j = 0; while (data_length--) { i = (i + 1) % 256; i = (i + 1) % 256; j = (j + S[i]) % 256; swap(S[i], S[j]); int t = (S[i] + S[j]) % 256; int k = S[t]; //k为加密密钥,直接进行与数据异或或者存进数组里最后进行异或都可以, }函数完整代码
#include<iostream> using namespace std; int S[256] = { 0 }; void swap(int& a, int& b) { int c = a; a = b; b = c; } void KSA(unsigned char key[], int len) { for (size_t i = 0; i < 256; i++) S[i] = i; int j = 0; for (size_t i = 0; i < 256; i++) { j = (j + S[i] + key[i % len]) % 256; swap(S[i], S[j]); } } void PRGA(unsigned char data[], int len) { int i = 0, j = 0, num = 0; int data_length = len; while (data_length--) { i = (i + 1) % 256; j = (j + S[i]) % 256; swap(S[i], S[j]); int t = (S[i] + S[j]) % 256; int k = S[t]; data[num] = (data[num] ^ k); num++; } } int main() { unsigned char key[] = "xwdidi.com"; unsigned char data[] = "bbspediycom"; KSA(key, strlen((char*)key)); PRGA(data,strlen((char*)data)); for (size_t i = 0; i < strlen((char*)data); i++) { cout << hex << (int)data[i] << " "; } return 0; }
初探逆向识别RC4
使用加密与解密中的RC4Sample进行分析学习.
主函数体伪代码
中间两个函数可能就是KSA和PGRA.
sub_401000
伪代码全图:
可以看中间do-while循环,有一个数组的256位初始化.说明a1+2是一个数组s-box的位置,那么*a1和a1[0]就是两个int型变量.然后下面的循环中,其实是交换和计算j是交叉在一起的.31,32,35,36是计算j的位置,30,33,34是交换.
通过v3与a3比较,获得对key长度取余的效果.v8则是每循环一次加一取值的s-box.
sub_401070
第一眼会发现做了异或操作,可能这就是PRGA.
仔细观察后发现result[2]其实是s-box的首地址,其他变量的话就是相对首地址的偏移.30,31,34,35,36其实交换函数.其他就是获得异或key所需的偏移计算.
魔改RC4
- 使用其它算法对参数进行加密,与其他加密算法糅合.
- S盒的内部数据固定
总结
对于循环,又有256或者0x100的关键字,获取字符串长度,又再次使用处理过的值进行异或的话可以去怀疑是RC4加密.
TEA
xtea,xxtea,tea都可以用0x9E3779B9识别,详细分析后面有空再写吧
AES
基本原理
分组长度:128比特
密钥长度:128, 192, 256比特
圈数:分别为10, 12, 14
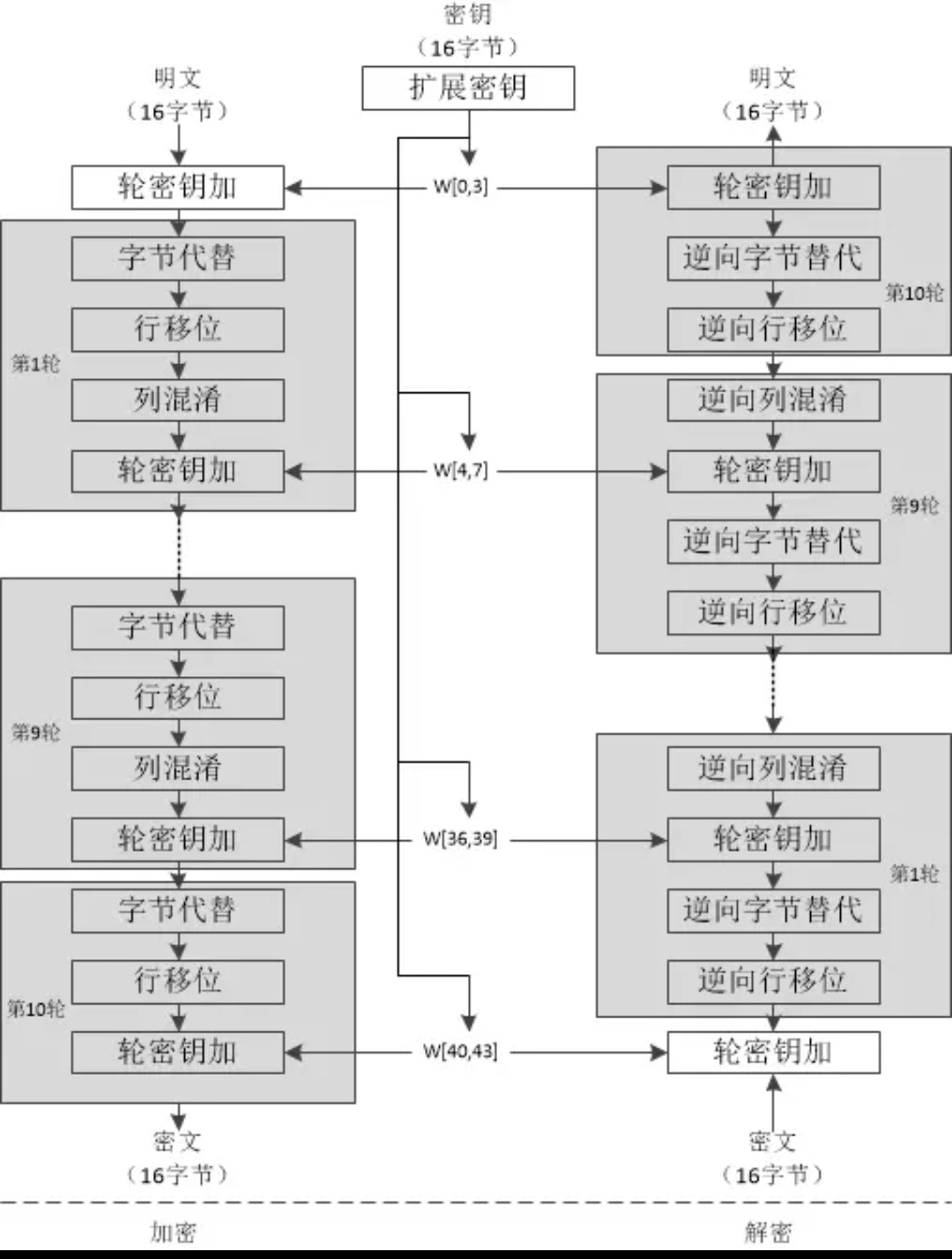
设定Nr为第r+1次轮函数. 将输入复制到状态数组中.在进行一个初始轮密钥加操作之后, 执行Nr次论函数.对状态数组进行变换, 其中最后一轮不同于前Nr-1 轮. 将最终的状态数组复制到输出数组中. 即得到最终密文(引用自加密与解密)
AES-128:
轮密钥加(AddRoundKey):将状态元素与轮密钥进行简单的异或计算,唯一需要三个参数的过程.
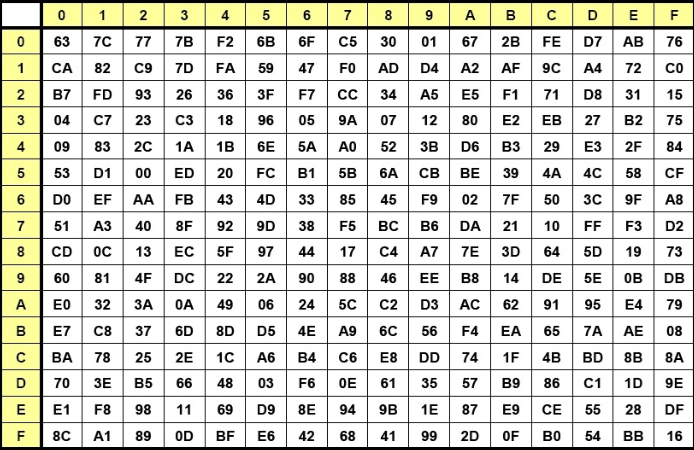
字节替代(SubBytes):使用S-box进行查表,字节替换操作。
S-box:
行位移(ShiftRows):数组大小为4x4字节,第一行保持不变,第二行循环左移1字节,第三行循环左移2字节,第四行循环左移3字节.
列混淆(MixColumns):以列为单位,可看作进行矩阵乘法,矩阵为((02,03,01,01)(01,02,03,01)(01,01,02,03)(03,01,01,02))
密钥扩展(KeyExpansion):通过密码扩展算法生成Nr+1个32位双字
解密就是逆过程了
空间换时间
大多数时候,常见aes使用空间换时间
将轮函数的几个步骤合并为一组简单的查表操作,只是最后一步没有,需要使用常规方法处理.
然后需要4个T表,一个T表需要256个4字节的32位双字,所以需要4kb的存储空间.
每进行一轮,4次查表,4轮异或运算.一共有四次,16轮查表,16轮异或
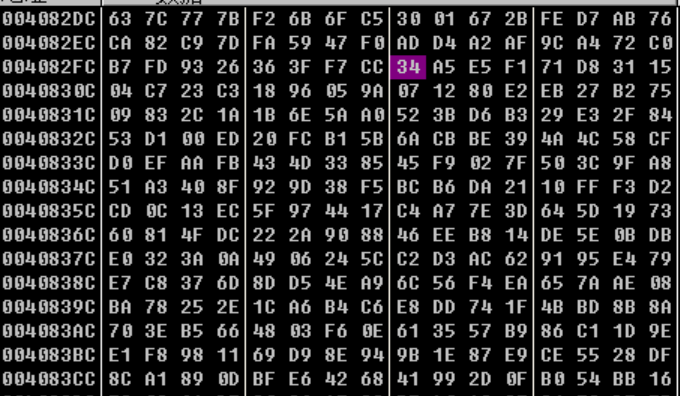
T表数据图
逆向初探识别RSA
一样使用的是加密与解密中的样例
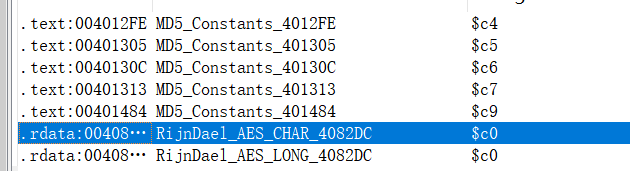
FindCrypt识别处MD5和AESSerial长度为32字节,使用16进制的话刚好为128位。静态分析大概这样,接下来动态看看
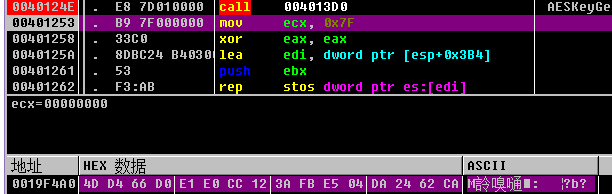
sub_401320压入初始化后的寄存器数组地址,name, 长度最终获得128位
MD5散列值执行
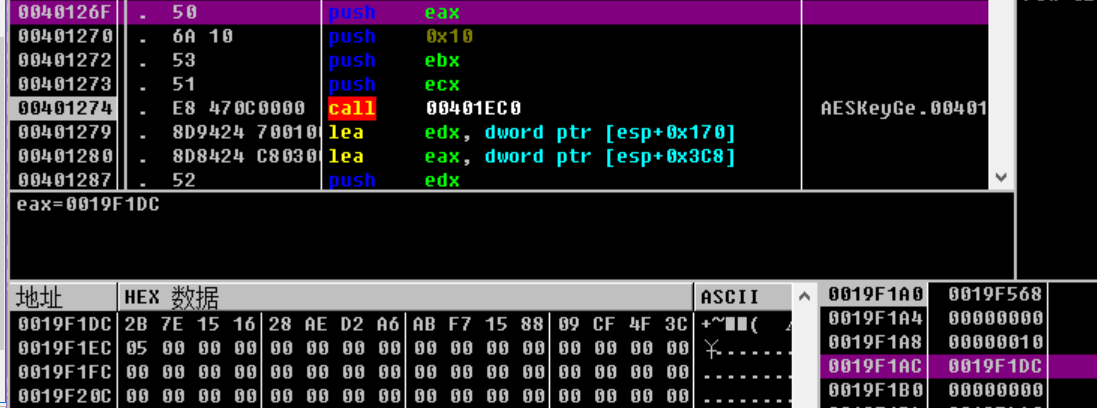
sub_401EC0内存中的
sbox细致算法省略
函数中存在大量的移位异或操作,太大了就不截图了.
注册机
加密模式与填充模式
- ECB: 需要加密的消息按照块密码的块大小被分为数个块,并对每个块进行独立加密。
- CBC : 每 个明文块先与前一个密文块进行异或后,再进行加密
- CTR
- OCF
- CFB
ECB 与 CBC
PKCS7Padding: 假设数据长度需要填充n(n>0)个字节才对齐,那么填充n个字节,每个字节都是n;如果数据本身就已经对齐了,则填充一块长度为块大小的数据,每个字节都是块大小。
PKCS5Padding:PKCS7Padding的子集,块大小固定为8字节
Zero-Padding 用0填充(适合以\ 0结尾的字符串加解密)
非堆对称加密
RSA
基本原理
选择两个不同大的质数
p和q,计算n=p*q根据欧拉函数,求得
r=φ(n)=φ(p)φ(q)=(p−1)(q−1)选择一个与
e互质且小于r的整数,并求得c关于r的模反元素,命名为d,有ed ≡ 1 mod r销毁
p和q,此时(n,e)为公钥,(n,d)为私钥$$
加密
加密 n^e ≡ c \bmod N,消息解密c^d ≡ n \bmod N \
(只需要证明n^{ed} ≡n\bmod N即可)
$$
逆向初探RSA
发现这个程序和书前文使用Miracl库运算的逻辑相同,那也简单分析一下.
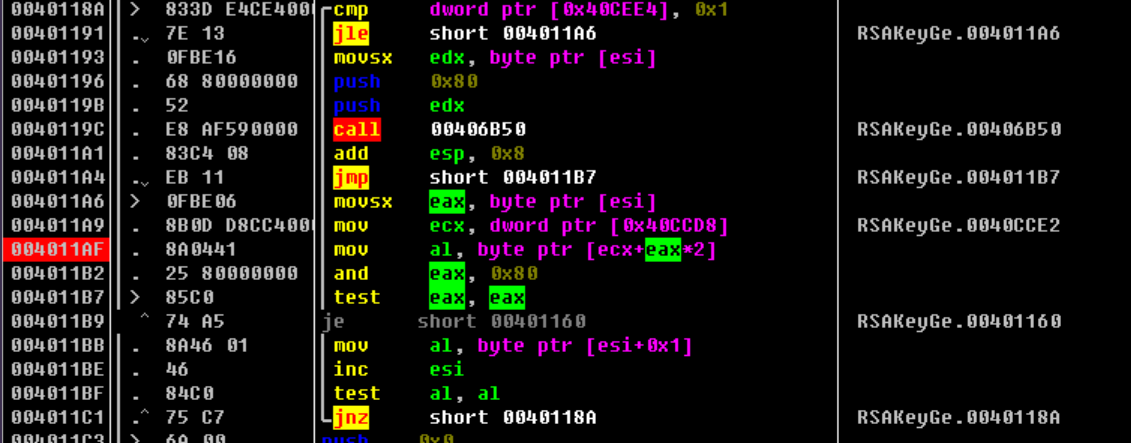
逐一检测数据是否为
0123456789abcdeABCDEF中的数据,如果有则直接报错参数初始化
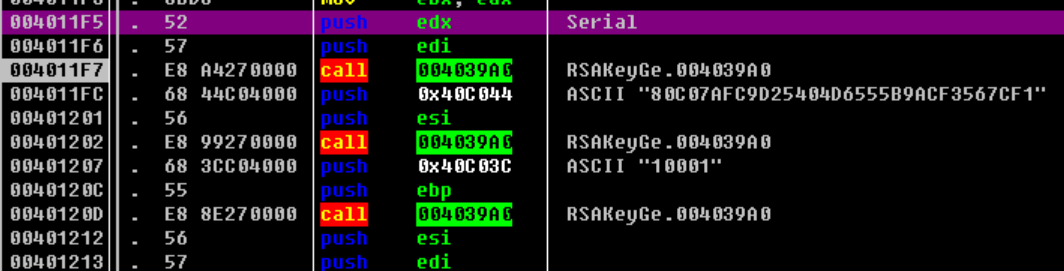
传入
Serial赋值m,大数n和e计算取模
比较判断是否正确
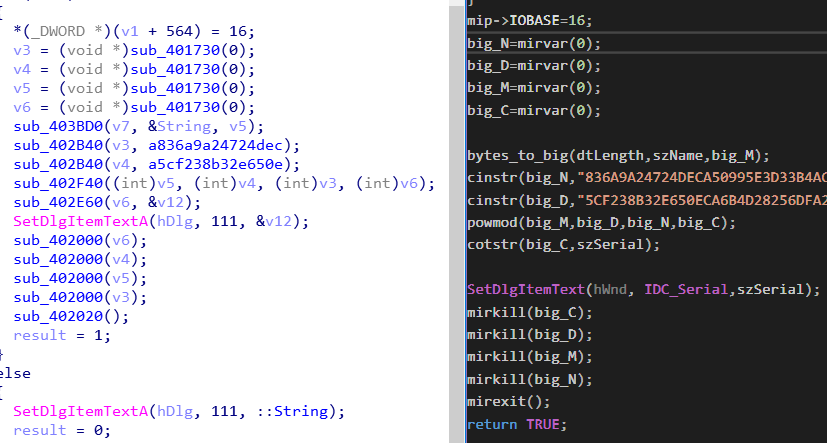
由此我们可知是将serial进行RSA解密与输入进行比较.得知了
n=0x80C07AFC9D25404D6555B9ACF3567CF1和e=0x10001使用大数分解
RSATool的Factor N功能,得到p=0xA554665CC62120D3,q=0xC75CB54BEDFA30AB输入
E,点击Calc. D得到d=0x651A40B9739117EF505DBC33EB8F442Dxwdidi的16进制为787764696469,使用大叔计算器进行c ^d ≡ m mod N计算,最后得到m=0x5D99FFF7B67285275C8639BCEF982B7,带入软件后返回Success!注册机
powmod函数的部分伪代码作为参考
Mircal大数运算库
Mircal库过于常用,需要进一步的熟悉才能更加利于分析.
头文件有mircal.h和mirdef.h两者,库文件为ms32.lib
以下是大数运算库函数的Magic number
反汇编识别
反汇编识别着重在于查看函数内部的mov doword ptr [eax+ecx*4+20], yy格式的反汇编代码,yy即为magic number
这是函数对比图
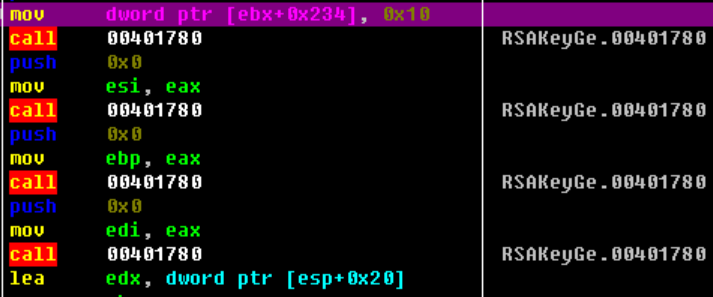
sub_401730
sub_403BD0
其他的就不一一找了,都在函数内部都能看见.基本上是这样去识别.
Reference
推荐
-

-

QQ空间
-

新浪微博
-

人人网
-

豆瓣



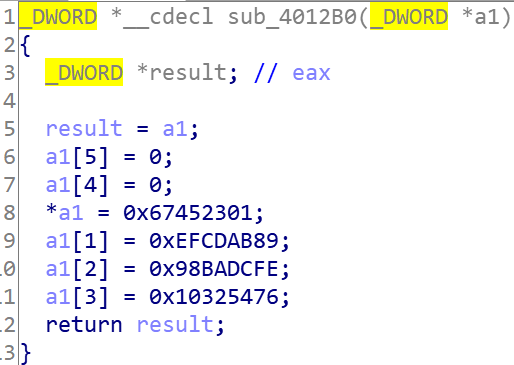 寄存器初始化
寄存器初始化
 进行回溯,
进行回溯,









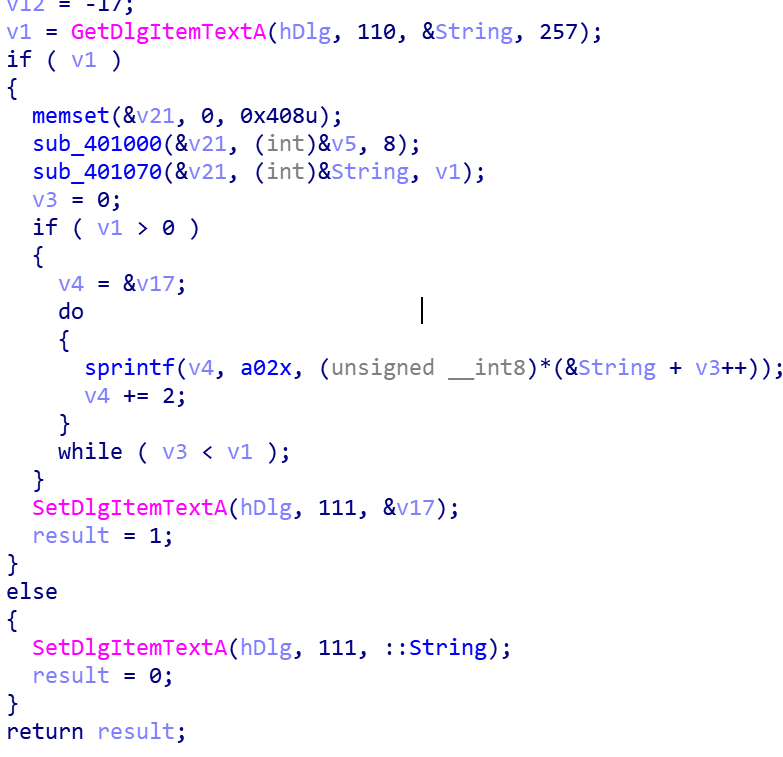 中间两个函数可能就是
中间两个函数可能就是




 函数中存在大量的移位异或操作,太大了就不截图了.
函数中存在大量的移位异或操作,太大了就不截图了.